「弱い」量子コンピュータを1量子ビットの追加でフルスペック化する新アプローチを開拓 ～量子計算における２つの万能性の差を世界で初めて解明～

発表のポイント：

光量子コンピュータの実現に有望な方式である測定型量子計算において、生成できる量子状態に制限がある「弱い」量子コンピュータに1量子ビット追加するだけで、制限がないフルスペックの量子コンピュータに変換する手法を世界で初めて開発しました。
本変換手法と既存の量子性の尺度を組み合わせることにより、生成できる量子状態に制限がある計算万能性と、制限がない量子状態万能性という重要な２つの性質の間にほぼ差がないことを明らかにしました。
これまで重点的に取り組まれてきた量子状態万能な量子コンピュータの開発を直接めざすアプローチとは異なり、本研究は計算万能な「弱い」量子コンピュータを経由する新しい開発アプローチを開拓しました。そのため本成果は、今後の量子コンピュータ理論の発展および実機開発に大きく貢献すると期待されます。

　日本電信電話株式会社（本社：東京都千代田区、代表取締役社長：島田　明、以下「NTT」）は、様々なタスクにおいて従来の古典コンピュータ（注１）よりも高速な計算を可能にすると期待されている量子コンピュータ(注２)の計算方式の中で、特に実現可能性が高い測定型量子計算(注３)において、出力できる量子ビット(注４)の状態に制限がある「弱い」量子コンピュータに１量子ビット追加するだけで、制限を完全に取り除きフルスペックにする手法を世界で初めて開発しました。本研究成果により、「弱い」量子コンピュータとフルスペック量子コンピュータの性能を表現する重要な概念である計算万能性（注５）と量子状態万能性（注６）の差が小さいことが明らかになりました。また、本成果は量子コンピュータの新しい設計方針を与えるものでもあるため、将来的には、量子コンピュータの実現や応用における課題を克服することに繋がると期待されます。

1．背景
　量子コンピュータは量子力学の原理に従い動作する次世代のコンピュータであり、物性物理、量子化学、暗号解読などに関する様々な問題を古典コンピュータよりも高速に解けると期待されています。これまで、量子回路（注７）を始めとして、様々な量子コンピュータの実現方式が提案されています。その中でも、測定型量子計算は光量子コンピュータの実現に特に適していることや、量子暗号（注８）などの様々な量子情報処理に応用できることから高い注目を集めています。測定型量子計算では、まず初めにリソース状態と呼ばれるエンタングル状態（注９）を準備し、それを1量子ビットずつ測定するという手順で量子計算を行います。つまり、本方式では、エンタングル状態を作るという難しい操作と、１量子ビット測定という比較的簡単な操作を必要とするステップが分離しています。量子回路の場合、このように綺麗に分離することは一般にできないため、これは測定型量子計算特有の利点です。この特性から、測定型量子計算は量子コンピュータのクラウド化にも有用であると考えられています（注１０）。クラウド化は、世界中の誰もがどこからでも量子技術の恩恵を受けられるための重要なアプローチです。
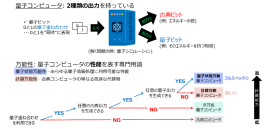
　これまでに複数提案されている量子計算方式に共通の特徴として、出力には、量子ビットを出力する量子出力と、古典ビットを出力する古典出力の２種類があります（図1）。特に、任意の古典出力は生成できるが量子出力には制限がある「弱い」量子コンピュータを計算万能と呼び、古典出力、量子出力ともに制限がないフルスペックの量子コンピュータを量子状態万能と呼びます。後者はあらゆる量子情報処理に使用可能という高い汎用性を有していますが、前者は計算の高速化など一部の用途にしか適用できないという課題があります。特に、複数の量子コンピュータを組み合わせて行う情報処理の中には、量子状態万能でないと行えないものがあることが知られています。その一方で、計算万能性は量子状態万能性よりも少ない種類の量子操作を使って達成できるため、実現が比較的容易だと考えられます。
　測定型量子計算の万能性は最初に準備するリソース状態で決まりますが、これまで計算万能なリソース状態と量子状態万能なリソース状態は、NTTを含めた様々な企業・大学により個別に発見されており、それらの万能性の間にどれくらいの差があるかということは明らかになっていませんでした。また、計算万能なリソース状態を量子状態万能なものに変換する方法もありませんでした。そのため、計算万能性しか持たない「弱い」量子コンピュータをまず初めに開発できたとしても、それを改良することで量子状態万能なフルスペック量子コンピュータを実現できるかは未解明でした。


[画像1]https://digitalpr.jp/simg/2341/106883/700_335_2025032809341567e5ee87382bb.PNG

図1：量子コンピュータの概要と２つの万能性。量子コンピュータには様々な種類がありますが、本研究では、量子状態万能性を有したフルスペックの量子コンピュータと、計算万能性を有する「弱い」量子コンピュータに着目しました。

2．研究内容
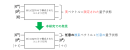
　今回、私たちは計算万能なリソース状態に1量子ビット追加するだけで、量子状態万能なリソース状態に変換する手法を考案しました（図2）。理想的には、「弱い」量子コンピュータさえ開発できれば、本変換手法を用いてリソース状態を少し改良するだけでフルスペック量子コンピュータの実現に繋がります。また、測定型量子計算ではどのような測定を行うかということも重要ですが、本変換手法では、必要な測定の種類が変換前後で変化しないという特徴も有しています。つまり、変換前後の違いは量子ビット１つ分だけであり、計算万能なリソース状態と量子状態万能なリソース状態にはほとんど差がないことが明らかになりました。特に、２つの万能性のリソース状態を、スタビライザ状態（注１１）からの遠さを表す尺度であるマジックで評価すると、値が同じになる場合があることも明らかにしました。このような意味でも両者の差は小さいと言えます。


[画像2]https://digitalpr.jp/simg/2341/106883/700_256_2025032809341567e5ee87379aa.PNG

図2：本研究成果のイメージ図。丸は1量子ビットを表しており、曲線で結ばれた2量子ビットはエンタングルしています。計算万能なリソース状態に含まれる適切な１量子ビットをパウリY固有状態|+i⟩≡(|0⟩+i|1⟩)/√2という特別な状態に置き換えることで、量子状態万能なリソース状態に変換できることを発見しました。

　量子計算はユニタリ行列（注１２）で表現することが可能であり、量子状態万能というのは任意のユニタリ行列を任意の高い精度で実現できることを意味しています。一方で、計算万能な場合は、直交行列など一部のユニタリ行列しか実現できません。本変換は、１量子ビット|+i⟩≡((|0⟩+i|1⟩))⁄√2を追加することで実行可能なユニタリ行列の種類を増やすというものになっています（図３，４）。簡潔にまとめると、私たちの研究成果は、１量子ビット追加するだけで量子コンピュータが実行できる操作が大幅に増えることを意味しています。図３から分かる通り、|+i⟩自体は変化しないにも関わらず、従来不可能だった任意の量子状態の生成が可能になることから、本成果は化学における触媒的変換のアナロジーになっていると考えることができます。


[画像3]https://digitalpr.jp/simg/2341/106883/700_271_2025032809364167e5ef19d8671.PNG

図3：本研究で示したことの概要。HとCCZはそれぞれ、アダマールゲートと制御制御Zゲートを表しています。計算万能な量子計算の場合、生成可能な量子状態は実ベクトルで表現できる限定されたものとなります。しかし、今回私たちは入力する量子ビットの内１つを|+i⟩に変更するだけで、任意の量子状態が任意の精度で生成可能になることを示しました。


[画像4]https://digitalpr.jp/simg/2341/106883/700_322_2025032809370367e5ef2fcd484.PNG

図4： |+i⟩を用いて位相ゲートSを実現する新手法。図3の変換を達成するために用いられます。(a) アダマールゲートHと制御制御ZゲートCCZのみを用いて|1⟩を生成するための量子回路。図中の縦線がCCZを表しています。(b) 変換手法によって追加した|+i⟩と(a)で生成した|1⟩を用いることで、HとCCZだけしか実行できない場合でも、任意の量子状態|ψ⟩にSを作用させることが可能となります。HとCCZとSを組み合わせることで任意のユニタリ行列を任意の精度で実現できるため、本回路を用いることによって量子状態万能性を満たすことができます。

　このような、量子ビットを追加することで情報処理能力を高める技術は量子情報分野で精力的に研究されており、量子誤り訂正で用いられるマジック状態注入（注１３）などが有名です。しかし、マジック状態注入では、量子アルゴリズムで用いられるユニタリ行列を実現する場合、問題のサイズに応じて追加する量子ビット数を増やす必要があります。一方で、本変換手法は、量子誤り訂正とは異なる用途で使用されるものの、問題のサイズに依らずに常に１量子ビットの追加しか必要としないというのが特徴です。

3．今後の展開
　今回提案した変換手法は、量子コンピュータの全ての機能を実現するためには、どのような要素技術が必要なのかを明らかにしました。ここで、要素技術は、測定型量子計算の場合、リソース状態の準備や量子ビットの測定などの操作に相当します。量子コンピュータの開発では各要素技術を高精度に実現する必要があるため、必要な要素技術を明らかにすることは重要です。今後も、本変換手法の改善・一般化を含め様々な角度から量子コンピュータ実現の課題克服に向けて理論面から取り組み、量子技術の早期実現に貢献します。特に、測定型量子計算は量子コンピュータのクラウド化に有用なため、本研究成果は、世界中の誰もがどこからでも量子技術の恩恵を受けられるような社会の実現に貢献すると期待できます。また、量子状態万能性は複数の量子コンピュータを用いる場合に特に重要であることから、本成果は複数の量子コンピュータによる量子情報処理の大規模化にも有用な可能性があります。

本研究への支援
　本研究は国立研究開発法人科学技術振興機構ムーンショット型研究開発事業 ムーンショット目標6「2050年までに、経済・産業・安全保障を飛躍的に発展させる誤り耐性型汎用量子コンピュータを実現」 （プログラムディレクター：北川 勝浩 大阪大学 大学院基礎工学研究科　教授）研究開発プロジェクト「誤り耐性型量子コンピュータにおける理論・ソフトウェアの研究開発（JPMJMS2061）」（プロジェクトマネージャー（PM）：小芦 雅斗 東京大学 大学院工学系研究科　教授）による支援を一部受けて行われました。

論文情報
雑誌名： Physical Review Letters （オンライン版：7月30日）
論文タイトル： Catalytic Transformation from Computationally Universal to Strictly Universal Measurement-Based Quantum Computation
著者： Yuki Takeuchi
DOI： https://doi.org/10.1103/PhysRevLett.133.050601
URL： https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.050601

【用語解説】
注１: 古典コンピュータ
現在普及しているコンピュータ。スーパーコンピュータも古典コンピュータの１種です。マクロな物質の運動を記述する古典力学の原理に従って動作するため、古典コンピュータと呼ばれています。

注２: 量子コンピュータ
ミクロな粒子がどう運動するかを記述する量子力学の原理に従って計算を行うコンピュータ。スーパーコンピュータなどの従来の古典コンピュータと比較して、飛躍的に高速な計算が可能だと考えられています。量子コンピュータが行う計算は量子計算と呼ばれます。

注３: 測定型量子計算
量子コンピュータ固有の計算方式。最初にエンタングル状態（注９）を準備し、それを1量子ビットずつ測定することで量子計算を行うことができます。特に光量子コンピュータ実現において有用だと考えられています。

注４: 量子ビット
量子コンピュータにおける情報の最小単位。古典ビットと違い、0と1が同時に存在しているかのような重ね合わせ状態など、量子力学特有の状態を取ることができます。

注５: 計算万能性（computational universality）
任意の量子回路の出力確率分布を生成できる能力のこと。ここでは特に、アダマールゲートHと制御制御ZゲートCCZと呼ばれる直交行列(要素が実数のユニタリ行列)を実行できる能力を意味しています。そのため、計算万能性だけでは、任意の量子状態を生成することはできません。

注６: 量子状態万能性(strict universality)
任意のユニタリ行列を任意の精度で実行できる能力を意味しており、この能力があればどんな量子状態も高精度に生成することができます。例えば、S≡|0⟩⟨0|+i|1⟩⟨1|と、計算万能性で実行可能なH,CCZを組み合わせることで量子状態万能性を達成できます。ユニタリ行列は直交行列を一般化したもののため、量子状態万能性は計算万能性よりも強い万能性です。

注７: 量子回路
量子コンピュータの動作を図示したもの。量子回路をもとに設計された量子コンピュータは量子ゲート方式と呼ばれることもあります。

注８:　量子暗号
量子力学の原理を利用している暗号プロトコルの総称。量子鍵配送や秘匿量子計算など様々なものが提案されています。

注９: エンタングル状態
２つ以上の量子ビットが取り得る状態で、量子力学特有の相関であるエンタングルメントを有していることを意味しています。量子もつれ状態とも呼ばれます。重ね合わせ状態とともに量子コンピュータに欠かせない量子状態です。

注１０: 測定型量子計算を用いたクラウド化
測定型量子計算は、エンタングル状態を作る難しい操作と、１量子ビット測定という比較的簡単な操作の２つから構成されています。前半の難しい操作を遠隔地の量子コンピュータに依頼し、後半の簡単な操作をユーザが行うことで、ユーザの計算内容が秘匿されたセキュアなクラウド量子計算を実現できることが知られています。

注１１: スタビライザ状態
スタビライザ群の全ての生成元の同時+1固有状態。スタビライザ群とは、パウリ群の可換部分群のうち、恒等行列に-1をかけたものを含まない群です。一般の量子状態と異なり、古典コンピュータ上で効率的に表現可能という特徴があります。そのため、量子コンピュータ実現には、スタビライザ状態ではない量子状態、つまりマジックが０ではない量子状態を生成できる技術が求められます。

注１２:　ユニタリ行列
複素正方行列の中で、自身の随伴行列と掛けることで恒等行列になるものをユニタリ行列と言います。特に、全ての要素が実数の場合は、直交行列と呼びます。

注１３: マジック状態注入
量子計算中に発生したエラーを訂正する手法である量子誤り訂正における重要な技術の一つ。非スタビライザ状態であるマジック状態を消費して行われます。本技術を用いることで、量子コンピュータに必要な全ての量子ゲートをフォールトトレラントに実行できます。